10158. Найдите центроид
Найдите любой центроид в дереве.
Вход. Первая
строка содержит одно целое число n (1 ≤ n ≤ 2 * 105)
– количество вершин. Каждая из следующих n – 1 строк
содержит по два целых числа vi и ui (1 ≤ vi, ui ≤ n) – вершины,
между которыми существует ребро.
Гарантируется, что этот граф – дерево.
Выход. Выведите
номер вершины, которая является центроидом. Если центроидов несколько, выведите
любой.
|
Пример входа |
Пример выхода |
|
12 1 3 2 3 3 4 4 5 4 6 6 7 6 10 10 11 10 12 6 8 8 9 |
6 |
РЕШЕНИЕ
поиск в глубину - центроид
Анализ алгоритма
Пусть
имеется дерево из n вершин.
Центроидом дерева называется такая вершина,
при удалении которой дерево распадается на компоненты связности, количество
вершин в каждой из которых не более n / 2.
В задаче
следует найти все центроиды дерева.
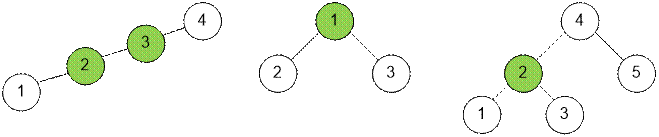
Рассмотрим
примеры деревьев и их центроиды (отмечены зеленым цветом).
Запустим
поиск в глубину dfs(v), который в sub[v] вычислит количество вершин
в поддереве с вершиной v. Для
приведенных примеров возле каждой вершины v
укажем соответствующее ей значение sub[v] (поиск в глубину стартуем во
всех примерах из вершины 1).
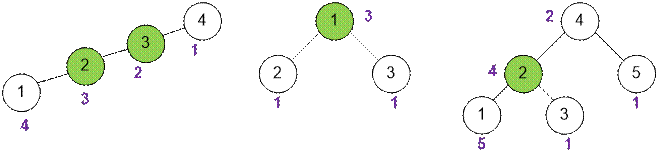
Если
вершина v имеет
сыновей to1, to2, …, tok
, то
sub[v] = 1 + sub[to1] + sub[to2] + … + sub[tok]
Вершина v является центроидом дерева тогда и только тогда,
когда:
·
для каждого ее сына to имеет
место sub[to]
≤ n / 2;
·
если
из дерева удалить поддерево с корнем v,
то оно будет содержать не более n / 2 вершин: n – sub[v] ≤ n / 2;
Например, в
правом на рисунке дереве с n = 5 вершинами центроидом будет вершина 2, потому что
·
sub[4] = 2 ≤ n / 2;
·
sub[3] = 1 ≤ n / 2;
·
n – sub[2] = 5 – 4
= 1 ≤ n / 2;
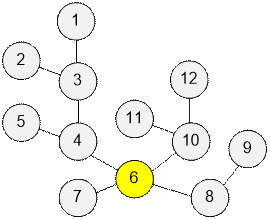
Пример
Рассмотрим дерево из примера. Вершина 6 является центроидом.
Реализация алгоритма
Граф будем хранить в списке смежности
g.
vector<vector<int> > g;
Функция
dfs возвращает количество вершин в поддереве с вершиной v и сохраняет это значение в sub[v].
int dfs(int v, int p = -1)
{
sub[v] = 1;
for (int to : g[v])
if (to != p) sub[v] += dfs(to, v);
return sub[v];
}
Функция
centroid совершает поиск в глубину, находит и заносит центроиды в
массив centr.
void centroid(int v, int p = -1)
{
Установим
flag = 1, если вершина v является центроидом.
int flag = 1;
Перебираем вершины to, смежные с v. Рассматриваем ребро v → to.
if (to != p)
{
Если
для сына to выполняется sub[to]
> n / 2, то v не является центроидом.
if (sub[to] > n / 2) flag = 0;
Если
для сына to выполняется sub[to]
< n / 2, то в поддереве с корнем to не содержится центроидов.
Есть смысл продолжать поиск в сыне to, если только sub[to] ≥ n / 2.
if (sub[to] >= n / 2) centroid(to, v);
}
Дерево без поддерева с корнем v содержит n – sub[v] вершин.
Если оно содержит более n / 2 вершин, то v не центроид.
if (n - sub[v] > n / 2) flag = 0;
Если для вершины v выполняются все условия центроида, то
заносим ее в массив centr.
if (flag) centr.push_back(v);
}
Основная
часть программы. Читаем входные данные. Инициализируем массивы.
scanf("%d", &n);
g.resize(n + 1);
sub.resize(n + 1);
Читаем
входной граф.
for (i = 0; i < n - 1;
i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Запускаем
поиск в глубину, ищем центроиды дерева.
dfs(1);
centroid(1);
Выводим
один из центроидов.
printf("%d\n", centr[0]);
Реализация алгоритма – второе решение
Запустим поиск в глубину dfs(v),
который для каждой вершины v вычислит
следующие величины:
· sub[v] содержит количество вершин
в поддереве с вершиной v;
· f[v] содержит максимальный
размер поддерева среди всех поддеревьев вершины v, включая поддерево, содержащее родительскую вершину v.
Тогда центроидом будет вершина v с наименьшим значением f[v]. Таких вершин может быть либо одна либо две в дереве.
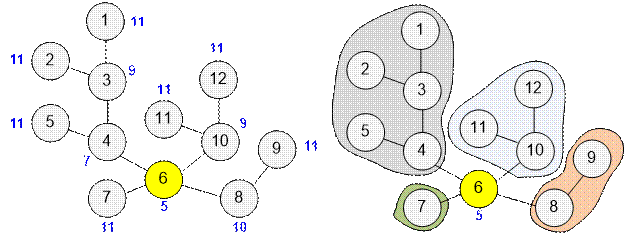
Вершина v = 6 соединена с 4 поддеревьями, размер
которых соответственно равен 1, 2, 3 и 5. Значение f[6] = 5 содержит максимальный размер поддерева.
В то же время
наименьшим значением в массиве f
является f[6] =
5. Следовательно вершина 6 является центроидом.
Рассмотрим расстановку
меток для дерева с двумя центроидами.
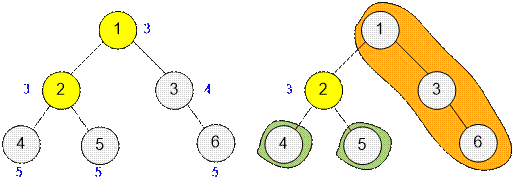
Две вершины имеют
наименьшее значение в массиве f: f[1] = 3 и f[2] = 3.
void dfs(int v, int p = -1)
{
sub[v] = 1;
f[v] = 0;
for (int to : g[v])
if (to != p)
{
dfs(to, v);
sub[v] += sub[to];
f[v] = max(f[v], sub[to]);
}
f[v] = max(f[v], n - sub[v]);
if ((root == 0) || (f[v] < f[root])) root = v;
}
Основная
часть программы. Читаем входные данные. Инициализируем массивы.
scanf("%d", &n);
g.resize(n + 1);
f.resize(n + 1);
sub.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a,
&b);
g[a].push_back(b);
g[b].push_back(a);
}
Запускаем
поиск в глубину, выводим один из центроидов дерева root.
root = 0;
dfs(1);
printf("%d\n", root);
Python реализация
Увеличим размер стека.
import sys
sys.setrecursionlimit(300000)
Функция
dfs возвращает количество вершин в поддереве с вершиной v и сохраняет это значение в sub[v].
def dfs(v, p = -1):
sub[v] = 1
for to in g[v]:
if to != p:
sub[v] += dfs(to, v)
return sub[v]
Функция
centroid совершает поиск в глубину, находит и заносит центроиды в
массив centr.
def find_centroid(v, p = -1):
Установим
flag = True, если вершина v является центроидом.
flag = True
Перебираем
вершины to, смежные с v. Рассматриваем ребро v → to.
for to in
g[v]:
if to == p: continue
Если
для сына to выполняется sub[to]
> n / 2, то v не является центроидом.
if sub[to] > n // 2:
flag = False
Если
для сына to выполняется sub[to]
< n / 2, то в поддереве с корнем to не содержится центроидов.
Есть смысл продолжать поиск в сыне to, если только sub[to] ≥ n / 2.
if sub[to] >= n // 2:
find_centroid(to, v)
Дерево без поддерева с корнем v содержит n – sub[v] вершин.
Если оно содержит более n / 2 вершин, то v не центроид.
if n - sub[v] > n // 2:
flag = False
Если для вершины v выполняются все условия центроида, то
заносим ее в массив centr.
if flag: centr.append(v)
Основная
часть программы. Читаем входные данные. Инициализируем массивы.
n = int(input())
g = [[] for _ in
range(n + 1)]
sub = [0] * (n + 1)
centr = []
Читаем
входной граф.
for i in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Запускаем
поиск в глубину, ищем центроиды дерева.
dfs(1)
find_centroid(1)
Выводим
один из центроидов.
print(centr[0])
Python реализация – второе решение
Увеличим размер стека.
import sys
sys.setrecursionlimit(200000)
Запустим поиск в глубину dfs(v), который для каждой вершины v вычислит следующие величины:
·
sub[v]
содержит количество вершин в поддереве с вершиной v;
·
f[v] содержит максимальный размер поддерева среди всех поддеревьев
вершины v, включая поддерево,
содержащее родительскую вершину v.
Тогда центроидом
будет вершина v с наименьшим
значением f[v]. Таких вершин может быть либо одна либо две в дереве.
def dfs(v, p=-1):
global root
sub[v] = 1
f[v] = 0
for to in g[v]:
if to != p:
dfs(to, v)
sub[v] += sub[to]
f[v] = max(f[v], sub[to])
f[v] = max(f[v], n -
sub[v])
if root == 0 or f[v] < f[root]:
root = v
Основная часть программы. Читаем
входные данные. Инициализируем массивы.
n = int(input())
g = [[] for _ in range(n + 1)]
f = [0] * (n + 1)
sub = [0] * (n + 1)
for _ in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Запускаем поиск в глубину, выводим
один из центроидов дерева root.
root = 0
dfs(1)
print(root)